

Aristóteles de Estagira (384 a.C. - 322 a.C.)
Tudo que está em movimento deve ser movido por algo. Pois se não tem a fonte de seu movimento em si mesmo, é evidente que é movido por outra coisa que não seja ele mesmo, pois deve existir algo que o mova. Se, por outro lado, se ele tem a fonte de seu movimento dentro de si, tomemos AB para representar o que está em movimento essencialmente por si mesmo e não em virtude do fato de que algo pertencente a ele está em movimento. Então, primeiramente, ao assumir que AB, por estar em movimento como um todo e não ser movido por nada externo a si mesmo, é movido por conta própria é como se, supondo que KL mova LM e também a si mesmo, fôssemos negar que KL é movido por algo sobre o chão de modo que não seja evidente qual é a parte que move e qual é a movida. Em segundo lugar, o que está em movimento sem ser movido por qualquer coisa não necessariamente cessa seu movimento, porque outra coisa está em repouso, mas uma coisa deve ser movida por algo se o fato de outra coisa ter cessado seu movimento levá-la a estar em repouso. Assim, aceitando-se isso, tudo que estiver em movimento deve ser movido por algo. Pois AB, que foi tomado para representar o que está em movimento, deve ser divisível já que tudo que está em movimento é divisível. Seja ele dividido em G. Então, se GB não está em movimento, então AB não estará em movimento: pois se o estiver, é claro que AG estaria em movimento ao passo que BG está em repouso, e assim AB não pode estar em movimento essencialmente e primariamente. Portanto, se GB não está em movimento, AB estará em repouso. Mas se concordamos que o que está em repouso se outra coisa não o move deve ser movido por algo. Consequentemente, tudo que está em movimento deve ser movido por algo: pois o que está em movimento será sempre divisível e se uma parte dele não se move, o todo deve repousar.Aristóteles, Física, livro VII, parte 1
Assim falou o grande filósofo grego a respeito do movimento dos corpos no plano. Se o raciocínio parece complicado, basta ficar com a frase inicial, pois todo o resto existe para justificá-la: "Tudo que está em movimento deve ser movido por algo." Tal como um arado cessa de sulcar a terra quando sua tração para. A relação entre o "poder motivo" e o deslocamento seria expressa uma relação simples:
Então, já que onde quer que haja um movente, seu movimento sempre age sobre algo, é sempre em algo e sempre se estende até algo (por "é sempre em algo", quero dizer que leva certo tempo; e por "se estende até algo" quero dizer que envolve percorrer uma determinada porção de distância, pois em qualquer momento que algo está provocando um movimento, ele já causou um movimento, de forma que sempre deve haver certa porção de distância que foi percorrida e certa porção de tempo que foi ocupada). A, o movente, deslocou B de uma distância G num tempo D, então no mesmo tempo e na mesma força, A moverá (1/2)B duas vezes a distância G e em (1/2)D moverá (1/2)B por toda a distância G: assim as regras de proporção serão observadas.Idem, livro VII, parte 5
Nesta parte de Física, ele tratou dos movimentos sobre o plano. Na direção vertical, os corpos aparentemente se movem sem que um agente interfira: pedras caem de penhascos ou a fumaça do fogo ascende ao céu. Para esses movimentos, Aristóteles lançou a ideia de lugar natural (cf. Fís, IV, 5): os corpos iam em direção à região mais afim com a essência dos elementos que o constituíssem. Desse modo, os corpos pesados naturalmente se deslocariam para o centro do planeta, onde se encontram os elementos mais pesados (terra e água), pois o "peso" seria uma característica intrínseca a eles, ao passo que os mais dotados de "leveza" tenderiam a se afastar do centro, em direção aonde predominassem os elementos mais sutis (ar e fogo). A rapidez desses dois tipos de movimentos naturais dependeria do meio em que o corpo se deslocasse e à quantidade de peso ou leveza que possuísse. Contudo, as forças resistentes ao movimento obedeceriam a uma razão inversa:
Portanto, o meio causa uma diferença porque impede a coisa em movimento, sobretudo se ela se move na direção oposta, mas em um grau secundário mesmo se ela estiver em repouso; e especialmente um meio que não seja facilmente divisível, i.e., um meio que seja um tanto denso. A, então, mover-se-á por B no tempo G e por D, que é mais fino, no tempo E (se o comprimento de B é igual ao de D), em proporção à densidade do corpo resistente. Pois seja B a água e D o ar; então, por tanto quanto seja o ar mais fino e mais incorpóreo que a água, A se moverá por D mais rápido que por B. Tenha a velocidade a mesma razão, pois, que o ar tem para a água. Então, se o ar é duas vezes mais fino, o corpo percorrerá B no dobro de tempo que faz em D e o tempo G será o dobro do tempo E. E sempre, por tanto quanto o meio seja mais incorpóreo e menos resistente e mais fácil de dividir, mais rápido será o movimento.Idem, livro IV, parte 8
Juntando-se esse dois últimos extratos de Física, pode-se chegar ao que seria uma formulação matemática do raciocínio do filósofo:
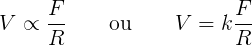
Onde V é a velocidade, F a força movente, R a resistente e k uma constante de proporcionalidade. Isso pode até parecer intuitivo, mas tem consequências curiosas. Se um objeto recebesse qualquer força movente em um meio sem resistência alguma - o vácuo - ele imediatamente adquiriria velocidade infinita! Um dos motivos, então, pelo qual Aristóteles rejeitou a possibilidade de existência do "vazio" na Natureza. Existem outras consequências dessa formulação que não seriam tão convenientes a ele, entretanto, que serão vistas mais adiante.
No caso do objetos arremessados (id.), que aparentemente se movem por conta própria por algum tempo, haveria uma "recolocação mútua" entre o projetil e o meio que em ele se desloca, que fluiria para sua retaguarda, empurrando-o à frente mais rápido que a locomoção para o lugar natural. Uma hora essa propulsão do meio de esgotaria em razão de forças de resistência dele mesmo e teria início, então, o movimento natural rumo ao solo. Não era possível a realização de dois movimentos simultaneamente (id., III, 3), nem havia possibilidade de "ação à distância" em sua filosofia da Natureza.
Uma flecha aristotélica.
Todos os movimentos descritos acima se processariam no chamado "mundo sublunar" - a região centrada na Terra e abaixo da Lua -, onde tudo estaria em constante movimento e mudança. Além dos movimentos naturais dos corpos graves e leves, havia um terceiro tipo, que era o movimento circular uniforme dos corpos celestes em torno da Terra. Numa teoria melhor desenvolvida em sua obra Sobre o Céu, Aristóteles estipulou que a Terra ocuparia o centro de uma série de esferas concêntricas - a mais próxima contendo a Lua, uma para cada planeta e o Sol, e, por fim, uma esfera mais externa para as estrelas. Essa, ao girar, transmitiria o movimento para as que lhe eram interiores, resultando no movimento dos astros. Nessa mesma obra, ele discute uma ideia também presente no último livro de Física: a existência de um primeiro motor. É uma conclusão um tanto lógica em seu sistema, afinal se tudo é movido por algo, então quem seria o primeiro a mover? Esse, além de mover a esfera das estrelas uniformemente, também teria propriedades divinas que o dispensariam de ser movido. Assim, o mundo sublunar seria regido por leis distintas das do celeste.
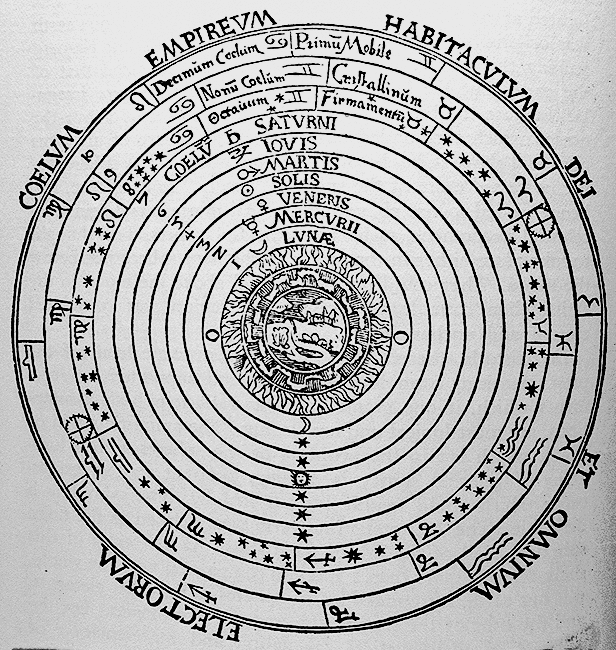
O Cosmos Aristotélico representado na Cosmographia Pedro Apiano, 1524
Preocupado mais em estipular as qualidades dos comportamentos dos corpos. Aristóteles nunca se interessou por quantificar, medir, experimentar ou confrontar teoria e fatos. Sua Física estava mais para uma especulação dialética do que uma ciência moderna. Embora sua Física (e outros tratados em diversas áreas do conhecimento) tenha(m) se revelado errônea(s), ele tem o grande mético de ter considerado o mundo com algo real. Ele o subdividiu em domínios hierárquicos, buscando princípios gerais a cada um a partir da análise de coisas concretas (ou tidas como tal), em vez de se debruçar sobre um suposto Mundo das Ideias, onde estariam as formas perfeitas dos objetos que conhecemos e do qual o nosso seria uma imperfeita e ilusória sombra, como fez seu antigo professor, Platão. Os pensamentos do mestre e do discípulo rivalizariam por séculos.

Detalhe do afresco A Escola de Atenas do pintor renascentista Rafael, em que se pode ver Platão, o mais velho e segurando um exemplar de sua obra Timeu, ao lado de Aristóteles, que segura Ética. Repare que a mão livre de Platão aponta para cima, o Mundo das Ideias, enquanto a de seu ex-discípulo se move para baixo.
Aristóteles passou boa parte da vida em Atenas - então centro cultural do mundo grego -, mas teve de lá fugir após de a morte do conquistador Alexandre Magno, de quem fora tutor, por medo de represálias. Faleceu em 322 a.C. na ilha de Eubeia, mar Egeu. Contudo, fundara quinze anos antes naquela cidade uma escola que seria conhecida como "Peripatética", que deu continuação e divulgação a sua linha de pensamento. Aristóteles se tornaria para as Ciências Naturais e a Lógica o que Euclides foi para a Geometria, Heródoto para a História e Hipócrates para a Medicina.
[índice]Com a conquista romana da Grécia em 146 a.C., a parte ocidental do Mediterrâneo travou contato com sua refinada cultura e saber. Os romanos sempre souberam aproveitar o que havia de melhor nos povos anexados a seu império e utilizaram sua tecnologia para melhorar a infraestrutura de seus vastos domínios, com a construção de estradas pavimentadas, aquedutos, fortificações, pontes, prédios públicos, portos, navios, etc. Contudo, os latinos se notabilizaram como engenheiros, homens de aplicação, e não realizaram grandes progressos por conta própria em pesquisa básica. A vanguarda científica continuou pertencente ao helenizado oriente, a parte mais culta de seu Império, que viu o florescer de outros centros de saber, como Alexandria, no Egito. Uma relativa prosperidade não só cultural, mas também econômica e política - a Pax Romana - durou de 27 a.C. a 180 da Era Comum. No período subsequente, a sociedade romana foi submetida à dura prova com uma série de imperadores ineptos, revoltas militares e epidemias, além de um intermitente assédio de tribos bárbaras ao norte e do Império Sassânida a leste. Diversas de reformas administrativas foram tentadas a partir do final do século III e, por fim, Teodósio I procedeu à definitiva divisão do império em suas metades oriental e ocidental. A primeira, o futuro e helenizado "Império Bizantino", resistiu ao ataques externos do V com êxito e perduraria com transformações até o século XV, com a tomada de Constantinopla pelos turcos otomanos. O ocidente, que sempre fora mais fraco em recursos humanos e econômicos, não resistiu às invasões bárbaras do século V e se esfacelou em uma série de pequenos reinos. O último imperador do ocidente - cujos domínios, grosso modo, já se limitavam ao que hoje são os territórios da Itália e da Croácia - foi deposto por um chefe bárbaro em 476 d.C. e esse episódio viria a ser considerado o marco final da Antiguidade clássica e o início da Idade Média.
Foi um período de desagregação do tecido social, com decréscimo populacional, da atividade econômica e da vida urbana. No âmbito cultural, ocorreu a elevação do cristianismo ao status de religião do império em seu penúltimo século de vida e a subsequente supressão do paganismo. A Igreja Católica imitou a organização impérial, mas, ao contrário dele, suas engrenagens funcionavam perfeitamente e foi a única instituição a sobreviver a sua queda. Como nova elite intelectual, coube aos clérigos a tarefa de preservar o legado greco-romano, mantidos em bibliotecas monásticas e lentamente multiplicados por monges copistas. Essa herança foi melhor preservada entre os bizantinos, mas eles não realizaram grandes avanços. Pelo contrário: desde o final da Antiguidade Clássica vinha se tornando comum a valorização da autoridade passada e tida como suspeita a inovação. Foi a entrada em cena de um terceiro grupo - os árabes - que realmente tirou a orla do Mediterrâneo e regiões adjacentes do marasmo intelectual. Conquistando, em poucas gerações, um império que se estendia da Índia à Espanha, eles e os povos islamizados criaram uma vasta área comum para o intercâmbio do conhecimento, com a tradução e difusão da filosofia grega, do sistema de numeração de posição criado pelos indianos e da fabricação do papel inventado pelos chineses. Todo esse florescimento cultural transbordou para a Europa a partir de três regiões onde se estabeleceram "culturas de contato" entre europeus e islâmicos: Espanha, Sicília e os reinos cruzados.
Se a fase das grandes invasões, que vai do século V ao X, foi destrutiva para a Europa, a partir do século XI começou-se um processo de reconstrução que se acelerou no século seguinte, com a retomada da atividade comercial e da vida urbana, muito devido a essa permuta. Melhorias tecnológicas aumentaram a produção agrícola e permitiram um aumento considerável da população, a difusão dos óculos dobrou a vida útil da mão de obra artesã, a introdução dos relógios deu um novo ritmo à atividade social, novos instrumentos permitiram aos navios ir mais longe com segurança e a arquitetura gótica produziu catedrais monumentais. Foi a época da fundação das primeiras universidades europeias: Bolonha (1088), Paris (ca. 1150), Oxford (1167), Cambridge (1209), Salamanca (1218), Montpellier(1220), Pádua (1222), etc. Algumas surgiram de corporações de professores que ofereciam seu serviços, outras como clubes de estudantes que contratavam mestres. Independentemente da estrutura, foi por meio delas que os leigos redescobriram os filósofos gregos, Aristóteles entre eles. Após o teólogo Tomás de Aquino (1225-1274) ter tornado o aristotelismo conciliável à religião cristã, atribuindo o papel de primeiro motor a Deus, seus tratados passaram a ser amplamente analisados e discutidos.
[índice]Em Oxford, foi fundado em 1264, pelo futuro bispo de Walter Merton, o núcleo do que originalmente se propunha ser uma faculdade de teologia, mais tarde conhecida com Merton College. No século seguinte, essa instituição produziria uma geração de pensadores responsável pelas primeiras tentativas de tratamento matemático às Ciências Naturais, o que lhes valeu o epíteto de Calculadores. Pode parecer estranho aos olhos modernos que homens versados no estudo do Divino pudessem se interessar por questões mais terrenas, mas, para filosofia desenvolvida nas universidades cristãs de então, era de crucial importância conciliar fé e razão. Nos estudos das leis naturais, justificativa para tanto pode ser encontrado na própria Bíblia, em Sb 11:20 "mas, dispusestes tudo com medida, quantidade e peso". Assim, o universo seria ordenado e, portanto, inteligível.
Nessa nova forma de ver as leis da natureza, destaca-se o nome de Thomas Bradwardine. Embora hoje mais lembrado por seus tratados teológicos sobre livre arbítrio e predestinação, por muito tempo entre os eruditos, seu nome esteve mais associado a sua obra Tratado sobre Proporções (1328), em que, entre outras coisas, aplicou esse ferramental matemático à física aristotélica. Bradwardine observou que a proposta original de V ∝ F/R demandava que o corpo atingisse imediatamente sua velocidade final tão logo a força movente atuasse e, além disso, ele estaria em movimento mesmo que a força resistente fosse igual ou maior que a movente. Sua velocidade diminuiria, de fato, mas nunca seria zero.
Para resolver esses problemas, Bradwardine propôs que a velocidade V crescesse aritmeticamente, ao passo que a razão F/R o fizesse geometricamente. Assim, quando dobrasse, F/R seria elevada ao quadrado; se V triplicasse, F/R iria ao cubo. Expressando matematicamente, isso seria:
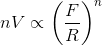
Sabendo que log ab = b log a, então a relação acima pode ser reescrita como:
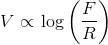
Óbvio que Bradwardine não se valeu do uso de logaritmos, que ainda não haviam sido descobertos, mas utilizá-los aqui facilita o entendimento para os leitores modernos. Se F = R, então V = 0; como esperado por ele. Caso a resistência se tornasse maior que a movente (o que ocorreria com n < 0), ter-se-ia uma velocidade negativa, o que ele interpretava como impossibilidade de movimento. Embora tenha sido engenhosa sua solução, é bom que se diga que ela é tão desprovida de base empírica como a de Aristóteles, a quem respeitava e não pretendia exatamente refutar, mas, sim, tentar corretamente exprimir a intensão original. Seu maior legado foram as técnicas que utilizou, com o uso implícito de relacionamentos funcionais, que constituíram um grande avanço ao que antes era quase pura retórica.
O ferramental desenvolvido por Bradwardine foi adotado pela geração seguinte de mertonianos - William Heytesbury, Richard Swineshead e John Dumbleton - que, entre diversos tratados filosóficos, se preocupou com questões de cinemática: a descrição qualitativa e quantitativa do movimento. Se para Aristóteles, qualidade e quantidade eram duas coisas distintas, os pensadores medievais achavam que uma alteração em alguma qualidade deveria ser acompanha de uma mudança de quantidade, por exemplo, um aumento da velocidade de um móvel (qualidade) implicaria no aumento da distância percorrida (quantidade). Foram classificadas assim as qualidades:
No último caso, a investigação dos mertonianos foi frustrada pela inexistência, à época, do cálculo diferencial, que só seria descoberto no século XVII. Quanto aos dois primeiros, chegaram a um importante resultado conhecido como "Regra de Merton", enunciado pela primeira vez, sem demonstração, no sexto capítulo de "Regras para a solução de Sofismas", de Heytesbury:
Quando a velocidade de um corpo em movimento cresce com um tempo de maneira que ela seja uniformemente deformada, em um dado período de tempo o corpo percorre o mesmo trajeto como se tivesse se movido uniformemente com a velocidade alcançada na metade do período.
Que é uma antecipação do "teorema da velocidade média", de Galileu. Apesar dos resultados alcançados, a tradição filosófica dos "calculadores" de Merton declinou a partir de meados do século XIV, talvez por desorganização da vida acadêmica em razão da Peste Negra ou por alguma falta de renovação de seus quadros, mas seus trabalhos seriam republicados e difundidos do outro lado do Canal da Mancha.
[índice]A Escola Parisiense é principalmente lembrada pelos nomes de Nicole Oresme e Jean Buridan, ambos clérigos e professores da universidade local. O primeiro (ca. 1320 - 1382) lecionou no Colégio de Navarra dessa instituição, foi tradutor de Aristóteles e autor de uma ampla gama de tratados, que iam da Cosmologia à Economia. Tal como os mertonianos, Oresme se valeu de ferramental matemático aperfeiçoado por ele mesmo, sendo precursor em diversos campos da "ciência dos números". Por exemplo, para melhor lidar com as relações entre qualidade e quantidade, Oresme lançou mão da Geometria: ele observou que a "quantidade", i.e, a distância percorrida por um objeto, poderia ser obtida através da área de uma figura geométrica constituída por um segmento horizontal (representando o tempo) de onde se levantariam perpendiculares correspondentes ao valor da qualidade (i.e., a velocidade) em um dado instante. Com isso, as qualidades uniformes seriam facilmente representadas por retângulos (a) e as uniformemente disformes por trapézios retângulos ou, caso começassem com intensidade nula, por triângulos (b).
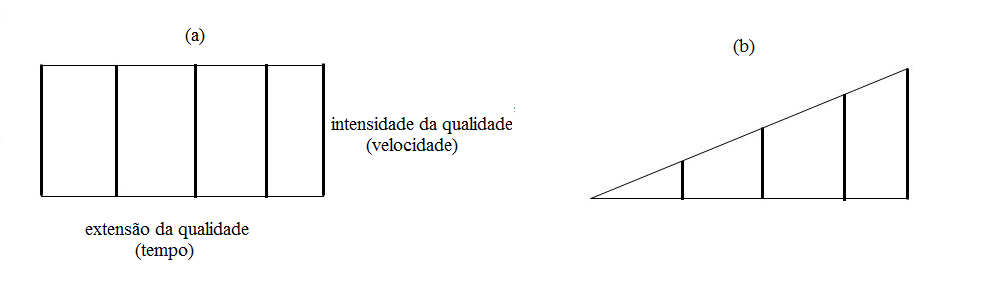
Diagramas de Oresme para qualidades uniformes e as uniformemente disformes. Adaptados de Tractatus de Configurationibus Qualitum et Motuum.
Oresme aplicou seu método geométrico na demonstração da Regra de Merton enunciada anos antes. Justapondo a figura para uma qualidade uniforme e outra de uma qualidade uniformemente disforme em cuja metade se atinja a mesma intensidade de qualidade da uniforme, ele constatou que a área das duas era a mesma

Demonstração geomética da Regra de Merton feita por Oresme. Idem.
Na pequena síntese De latitudinibus formarum ("Sobre a latitude das formas"), Oresme, ou algum discípulo seu, deu um passo adiante na generalização do método, trocando as figuras geométricas por uma espécie gráfico de barras, em que a extensão da qualidade era chamada de longitude e sua intensidade de latitude. Isso era, aproximadamente, a representação gráfica de uma função de uma variável independente com os eixos das abscissas e ordenadas, antecipando a geometria analítica de Descartes. Embora não justificasse, o autor intuía que, no caso da velocidade, a área sobre curva significava a distância percorrida em determinado tempo. A divisão em pequenas barras permitia, portanto, uma integração numérica simples para as qualidades disformemente disformes. Foi uma obra consideravelmente popular nos meios acadêmicos da época, sendo copiada e, posteriormente, impressa até o século XVI.
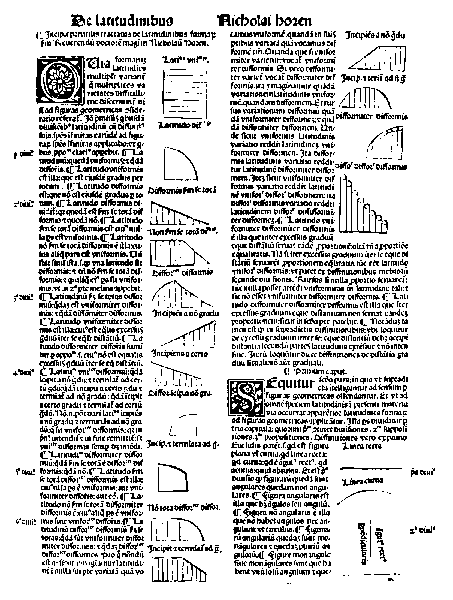

Uma página de uma edição impressa de De latitudinibus (esq.) e um detalhamento.
O que Nicole Oresme foi para a cinemática, seu veterano Jean Buridan foi para a dinâmica, fazendo o mais marcante avanço no estudo das causas do movimento até então. Não que inexistissem tentativas de revisar Aristóteles: já no século VI, o filósofo bizantino João Filópono escreveu um comentário à Física em que teceu um questionamento empírico à ideia aristotélica de o próprio meio o que impulsionava um projetil, após a perda de contato com o movente. Se, por exemplo, o ar saía da dianteira de uma flecha, ia para retaguarda e a impulsionava à frente, então porque não bataria colocá-la sobre um apoio e abanar em sua traseira para que se movesse? Essa falha empírica simples, mas crucial, levou Filópono a propor que o movente – seja ele a mão que atira uma pedra ou a corda do arco sobre a flecha – transferiria um uma espécie de poder cinético - enérgeia - ao corpo arremessado, que o manteria em movimento. O papel do meio seria meramente resistivo, desgastando a enérgeia até que o corpo parasse.
Essas ideias foram retomadas pelo professor da Universidade de Paris Jean Buridan (ca. 1300 – ca. 1360), em seu livro Sutilíssimas Questões sobre os oito Livros de Física de Aristóteles:
Sempre que algum agente põe um corpo em movimento, transmite a ele certo impetus, certo poder capaz de mover o corpo ao longo da direção imposta a ele na partida, seja para cima, abaixo, para o lado ou num círculo. Quanto maior a velocidade que é dada ao corpo pelo agente motor, mais poderoso será o impetus que lhe é dado. É esse impetus que move uma pedra depois de ela ter sido arremessada até o final do movimento. Mas por causa da resistência do ar e, também, de seu peso, que desvia o movimento da pedra numa direção diferente daquela a que o impetus é efetivo, esse impetus decresce continuamente. Consequentemente o movimento da pedra diminui sem interrupção. Finalmente, o impetus é sobrepujado e destruído no ponto onde a gravidade o domina e, daqui em diante, a última move a pedra em direção a seu lugar natural. (…).
Todas as formas e disposições naturais são recebidas pela matéria em proporção a ela mesma. Consequentemente, quanto mais matéria um corpo contiver, mais impetus pode ser transmitido a ele e maior a intensidade do impetus que pode receber (…) Uma pena recebe um impetus tão fraco que esse é destruído pela resistência do ar. Da mesma maneira, se alguém arremessa projetis e põe em movimento com igual velocidade um pedaço de madeira e outro de ferro, que tenham o mesmo volume e a mesma forma, o pedaço de ferro viajará mais longe por causa de o impetus que lhe foi transferido ser mais forte. É pela mesma razão que é mais difícil parar uma grande roda de ferreiro, a mover-se rapidamente, do que uma menor. (…)
Jean Buridan, citado por [Dugas, pp. 49-50]
Embora não tenha feito uma formulação matemática, é fácil deduzir dos textos acima que:
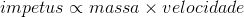
Essa formulação implícita dava à teoria do impetus um poder de explanação inimaginável na dinâmica aristotélica, e não apenas para fenômenos cotidianos, como arremessos e saltos, mas também a fenômenos físicos mais profundos, como a gravidade - que aceleraria um corpo por transferir-lhe continuamente impetus - ou o movimento dos corpos celestes. Para Buridan, não seria necessária a ação constante de um primeiro motoro para manter as esferas celestes em movimento. O primeiro motor - Deus, na interpretação cristã - teria apenas dado um impetus inicial às esferas e desde então, devido à ausência de resistência, elas permanecem em movimento.
O grande divulgador da teoria do impetus foi seu discípulo Alberto da Saxônia [Crombie, Vol. II, cap. III, pp. 86-7], discípulo de Buridan e, posteriormente, reitor da Universidade de Paris. Como inovação, ele a aplicou para descrever a trajetória de projetis por meio da "composição de impetus":
Embora seja uma descrição nada acurada de como os projetis realmente se comportam, essa teoria descreve, grosso modo, a trajetória de corpos menos densos e, portanto, muito suscetíveis à resistência do ar como, por exemplo, petecas. Assim, ela foi aceita por nomes como Blasio de Parma, Nicolau de Cusa, Leonardo da Vince e, com algumas modificações, pelo matemático Nicolau Fontana (vulgo, Tartaglia).
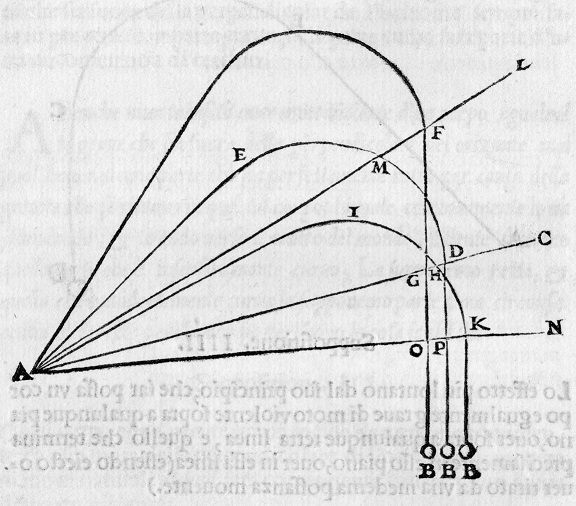
Figura extraída de La Nova Scientia, de Nicolau Tartaglia, 1537.
Alguns poderão reparar que a formulação do impetus lembra a da conservação da quantidade movimento (ou momento linear). Contudo, há diferenças cruciais:
Apesar desses problemas, essa teoria teve boa aceitação entre o fim da Idade Média e o começo da Moderna, até porque se enquadra no que os cientistas cognitivos chamam de física intuitiva: a bagagem mental com que cada ser humano nasce e que lhe permite estimar como os objetos "caem, ricocheteiam e vergam" [Pinker, XIII, pp. 303, 307]. Seria preciso o advento de alguém capaz de enxergar "fora da caixa" para a Física dar um passo adiante.
[índice]
Galileu Galilei (1564 - 1642)
Após sua condenação e retratação forçada de suas crenças heliocêntricas (i.e., o Sol como centro do sistema planetário), o físico, matemático e astrônomo Galileu Galilei passou seus últimos dias confinado a uma espécie de prisão domiciliar. Isso não significa que passou esse tempo inativo, pois foi quando redigiu Discursos e Demonstrações Matemáticas Relativas à Duas Novas Ciências (1638), em fez que um apanágio de suas pesquisas em mecânica. Nelas, Galileu deu grande ênfase na observação e experimentação, o que lhe custou desgastantes debates com os, por eles chamados, "filósofos in libris": os meros repetidores dos livros antigos, principalmente os de Aristóteles, colocando uma pretensa autoridade tradicional acima dos resultados práticos. O uso da experimentação não era exatamente uma novidade - tenha certeza que o anônimo inventor da roda penou um pouco até descobrir que o atrito por rolamento era menor que o por deslizamento -, mas foi Galileu quem popularizou o emprego de experimentos como parte da argumentação, coisa a que os neoaristotelistas eram refratários.
Um dos experimentos de Discursos... - explanado terceiro dia da narrativa, problema IX, proposição XXIII - foi particularmente desconcertante às ideias da Física de Aristóteles. Sejam dois planos inclinados conectados em forma de V. Quando uma esfera for solta do topo de um deles, ela adquire velocidade em razão da gravidade, mas não se deterá ao fundo. Em vez disso, tornará a subir pelo segundo plano. Quanto mais polida for a superfície, mais próxima a esfera chega à altura original, no segundo plano. Daí Galileu postulou que esfera oscilaria indefinidamente entre um plano e outro, caso fosse suprimido qualquer atrito. Caso se aumentasse progressivamente o ângulo entre os planos, a esfera percorreria uma distância cada vez maior antes que chegar à altura de lançamento e com uma desaceleração mais lenta. No caso limite, com um dos planos na horizontal, a esfera rolaria indefinidamente, em linha reta, com a velocidade atingida ponto mais baixo, se não houver forças de resistência ou que o impulsionem.
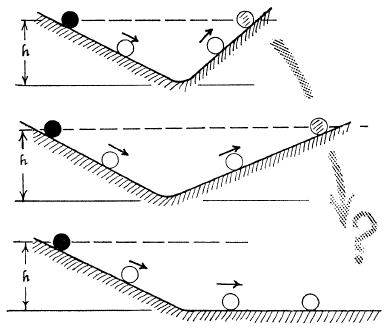
Galileu não foi o primeiro a propor o movimento retilíneo uniforme para um corpo sobre um plano e livre da ação de forças - a teoria do impetus já postulava algo semelhante -, contudo foi pioneiro ao expor isso em bases experimentais e mais: ao passo que, para os filósofos medievais e os neoaristotelistas da Renascença, o movimento era um estado transitório de um corpo enquanto não retornava ao seu lugar natural, Galileu considerou o movimento uniforme em certa direção como o comportamento padrão na Natureza de um corpo uma vez perturbado. Ele não estava preocupado com as qualidades específicas de uma esfera rolante, mas com a atuação de uma força inerente ao corpo chamada peso e com a ação do meio sobre o movimento. A primeira, contudo, não deteria o corpo caso ele adquirisse alguma velocidade horizontal. Essa independência entre a queda dos corpos e de seu movimento em outras direções foi fundamental para sua defesa do movimento da Terra em torno do Sol, pois nós, em nossa experiência usual, ignoraríamos que estamos em movimento, tal como um marinheiro, dentro do porão de um navio e em mar tranquilo, não sabe dizer se está ancorado ou velejando sob vento regular. Na falta de qualquer referencial, repouso e movimento uniforme são indistintos.
Embora se reconheça que essas ideias formaram o embrião do chamado "Princípio da Inércia", essa última palavra não aparece em lugar algum dessa obra. Na verdade, a primeira pessoa a difundir essa palavra no meio científico foi um contemporâneo de Galileu e parceiro de heliocentrismo, com quem trocara vasta correspondência, o astrônomo e matemático Johannes Kepler (1571 — 1630). Em seu tratado Epítome da Astronomia Coperniquiana, cap. IV, declara:
Mesmo que um globo celestial não seja pesado no sentido em que uma pedra sobre a terra é dita pesada e não seja leve como entre nós se diz que o fogo seja leve, tem, contudo, em razão de sua matéria, uma αδυναμια ou impotência natural para cruzar de um lugar a outro e tem uma inércia natural, ou inação pela qual repousa em todo lugar onde seja posto sozinho. E, portanto, a fim de que possa ser retirada de sua posição e sua inação, é necessário algum poder que deva ser mais forte que sua matéria e seu corpo puro, e que deva se sobrepor à sua inércia natural. Pois tal faculdade está acima da capacidade da natureza e é um desabrochar da forma ou um sinal de vida.
Para Kepler, portanto, a inércia seria apenas a resistência de um corpo a sair da condição repouso e estaria relacionada à massa, i.e., a quantidade de matéria nele existente. Já nos prenúncios do movimento Iluminista, o filósofo francês René Descarte (1596 - 1650), em seus Princípios de Filosofia (1644), propôs que repouso e movimento poderiam ser as duas faces da mesma moeda:
Parte II - Os Princípios das Coisas Materiais.
- O Movimento não requer mais ação alguma do que o repouso.
- O movimento e o repouso são meramente modos variados de um corpo em movimento.
- (...)
- A primeira lei da natureza: cada coisa quando deixada por si continua no mesmo estado, portanto qualquer corpo em movimento continua a se mover até que algo o pare.
- (...)
- A segunda lei da natureza: cada coisa em movimento, se deixada a si mesma, move-se me linha reta, portanto qualquer corpo se movendo em círculo sempre tende a se afastar do centro círculo.
A grande síntese dessa ideias foi feita pelo físico inglês Isaac Newton (1643 - 1727) em seu livro Princípios Matemáticos da Filosofia Natural (1687), em cujo capítulo inicial apresentou as três "leis do movimento" sobre as quais assentaria seu raciocínio. A primeira delas, também conhecida como Princípio da Inércia, enuncia:
LEI I.
TODO CORPO PERSEVERÁ EM SEU ESTADO DE REPOUSO, OU DE MOVIMENTO UNIFORME EM LINHA RETA, A MENOS QUE SEJA OBRIGADO A MUDAR ESSE ESTADO POR FORÇAS IMPOSTAS SOBRE ELE.
Projetis perseveram em seus movimentos, enquanto não forem retardados pela resistência do ar, ou impelidos para baixo pela força da gravidade. Um pião, cujas partes pela coesão são perpetuamente desviadas de movimentos uniformes, não interromperá sua rotação, se não fosse retardado pela resistência do ar. Os corpos grandes dos planetas e cometas, encontrando menos resistência em espaços mais livres, preservam seus movimentos, tanto progressivo quanto circular, por um tempo mais longo.
Vale notar que Newton tratou suas leis como axiomas, ou seja, proposições não demonstráveis, mas tidas como verdadeiras e pelas quais o restante será deduzido. Não vieram de uma espécie de insight filosófico, mas como uma generalização dos resultados dos cientistas que lhe antecederam.
[índice]Se pudéssemos levar determinado corpo para o espaço interestelar, livre de qualquer atração gravitacional significativa e de qualquer resistência atmosférica, e de lá dar-lhe uma impulsão inicial, ele adquiriria um movimento retilíneo uniforme no ponto de vista de algum ponto que fosse considerado fixo em relação às estrelas distantes. A longo prazo, prosseguiria indefinidamente rumo ao infinito ou até algo interferir em sua trajetória.
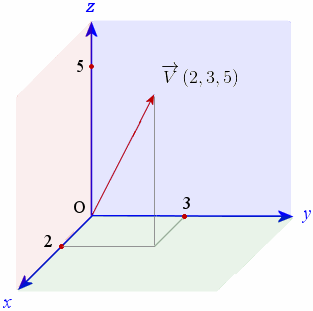
O vetor velocidade de um corpo livre no espaço.
Em nossa vivência usual, seria inviável realizar tal verificação experimental do Princípio da Inércia, por outro lado, ao relê-lo, é fácil constatar que ele não exige uma ausência total de forças atuando sobre o corpo, mas que elas não interfiram em seu estado de repouso ou movimento. Portanto, se as forças se cancelarem e/ou forem desprezíveis, pode-se esperar o mesmo resultado. Na superfície terrestre, o peso pode ser facilmente equilibrado pela força normal de contato de um plano horizontal e o atrito reduzido por polimento das superfícies. A resistência do ar, por sua vez, pode ser desconsiderada, por algum tempo, para um corpo compacto e denso, a se mover em baixa velocidade. Contando-se com equipamento especial, um experimento nessas condições pode ser realizado:
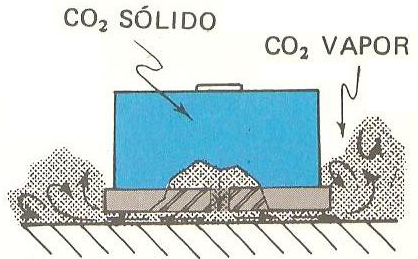
Fonte: [Alvarenga & Máximo, p. 179]
Um pesado disco de metal altamente polido na face inferior carrega um recipiente contendo gelo seco (CO2 sólido) que, ao evaporar, escapa por um orifício ao centro do disco. Isso cria um camada gasosa entre o disco e a superfície com a qual está em contato, permitindo que se descoloque sobre ela praticamente sem atrito, como mostra a foto estroboscópica abaixo.
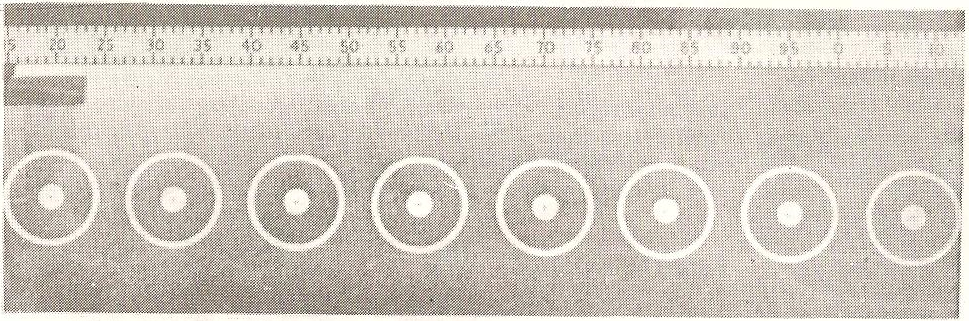
Fonte: Idem.
Existe uma versão mais modesta desse experimento que utiliza um colchão de ar comprimido, em vez de gelo seco, e um disco de plásito comum: o jogo de air hockey, com o qual o leitor talvez já tenha se divertido.
 |
 |
Embora este simplíssimo modelo de projetil, seja em forma laboratiorial ou algo mais lúdico, não tenha aplicação prática para a Artilharia, ele é um importante lembrete de que não se precisa de forças para manter um projetil em movimento. Elas são necessárias, sim, para causar alguma aceleração, i.e., uma mudança na intensidade e/ou sentido de sua velocidade, como aquela provocada pela força presente em todos demais tipos de projetil: a gravidade.
- Alvarenga, Beatriz & Máximo, Antônio; Curso de Física, Vol. I, Harbra, 3ªed., 1992.
- Aristóteles, Física, Internet Classics Archive, acessado em 14/10/2014
___________, Sobre os Céus, Internet Classics Archive, acessado em 14/10/2014
- Bianchi, Luca; A Física do Movimento, A Ciência na Idade Média, Scientific American Brasil: Especial História, nº1, pp. 40-3, Duetto, 2005.
- Crombie, Alistair Cameron; The History of Science: from Augustine to Galileo, Dover Publications, 1995.
- Dugas, René; A History of Mechanics, tradução inglesa de M.R. Maddox, Routledge & Kegan Paul LTD., Inglaterra, 1957.
- Hawking, Stephen; Os Gênios da Ciência - sobre os Ombros de Gigantes, Campus, 2005 [contém traduções em português de obras de Copérnico, Galileu, Kepler, Newton e Einstein, prefaciadas por Hawking].
- Pinker, Steven; Tábula Rasa, Companhia das Letras, 2002.
- Simonyi, Károly; A Cultural History of Physics, Taylor & Francis Group, 2012.
- Thakkar, Mark; The Oxford Calculators, Oxford Today, pp. 24-6, Trinity Issue, 2007.